Archiv der Kategorie: Weblog

Ungenügende Risikoangaben der Schweizer Onlinebroker

Veröffentlicht am von

Was bei Lebensmittel- und Pharmaindustrie so nicht ist

Wären Sie glück­lich, falls die Lebensmittelindustrie auf den Produktaufdruck der nähr­wert- und gesund­heits­be­zo­ge­nen Angabe ver­zich­ten wür­de. Dafür wür­de die Lebensmittelindustrie nach gehäuf­ten Lebensmittelerkrankungen eine Broschüre mit dem Titel “Besondere Risiken bei Lebensmittel” in die Haushaltungen verschicken.

Was wür­den Sie dazu sagen, wenn der Beipackzettel bei den Medikamenten nur das Anwendungsgebiet, die Dosierung bzw. Dauer der Anwendung und die Haltbarkeit des Medikamentes aus­wei­sen wür­de. Keine Hinweise auf die mög­li­chen Nebenwirkungen, Wechselwirkungen mit ande­ren Medikamenten usw. Sie wür­den aber nach gehäuf­ten Todesfällen ver­ur­sacht durch Medikamente von der Pharmaindustrie ein Heft mit dem Titel “Besondere Risiken bei Medikamenten” nach­hau­se geschickt bekommen.

Um beim Vergleich der Schweizer Onlinebroker zu blei­ben, es wäre durch­aus mög­lich die feh­len­den Informationen der Lebensmittel bzw. der Medikamente mit­tels Internet umständ­lich zu ermitteln.

Nicht nur die Rendite zählt 

Wahrscheinlich haben vie­le Anleger im Jahr 2008 und teil­wei­se auch 2009 schmerz­lich erfah­ren, dass die Rendite nur ein Teil einer Finanzanlage ist und das Risiko oft­mals zu wenig beach­tet wird.

effektenhandel

Ende 2008 und Anfang die­ses Jahres bekam ich von den Banken, wo ich online Wertschriften hand­le, das Heft “Besondere Risiken im Effektenhandel”. Wahrscheinlich habe fast alle online Trader von ihren Brokern eine sol­che Druckschrift erhal­ten. Erstaunlicherweise wur­den die Anleger erst mit dem Börsenabsturz 2008 wie­der ein­mal an die­se Risiken erinnert.

Angenommen Sie gehen zum ers­ten Mal zu einem Anlageberater, dann wer­den Sie hof­fent­lich fest­stel­len, dass er viel Zeit ver­wen­det, um Ihr Risikoprofile zu ermit­teln. Zusätzlich zu Ihrer Risikoneigung wird der Anlageberater auch Ihr erwar­te­tes Renditenziel und den unge­fäh­ren Anlagehorizont wis­sen wol­len. Mit die­sen drei Parametern, aus­ge­drückt in Zahlen, kann eine Finanzanlage bzw. ein Portfolio ermit­telt wer­den. Die meis­ten Wertpapiere haben ein Risiko/Rendite Profil, was viel­fach aus his­to­ri­schen sta­tis­ti­schen Kursen errech­net wird. Der Anlageberater wird auf Grund die­ses quan­ti­ta­ti­ven Anlageprozess, eines für Sie pas­sen­des Portfolio ermitteln.

Keine Risikoangaben bei Schweizer Onlinebroker

Leider küm­mert sich der Schweizer Onlinebroker wenig um das ein­ge­gan­ge­ne Risiko ihrer Kundschaft. Ich habe ein­mal ein paar Onlinebroker dar­auf hin geprüft, wel­che Risikozahlen sie beim Kauf eines Wertpapiere angeben.

Migros Bank

migros_no_risiko
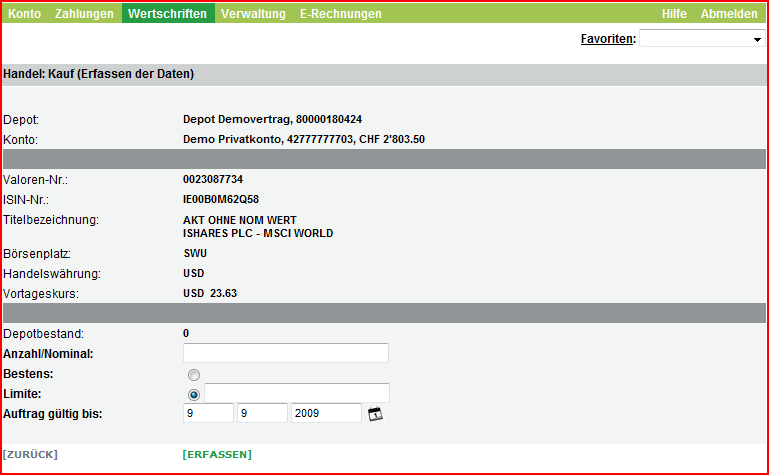
In ihren M‑BancNet gibt es weder beim Kauf eines Wertpapieres noch für das gesam­te Portfolio irgend­wel­che Zahlen über Risiken.

E‑Trading der Postfinance

etrading_no_risiko

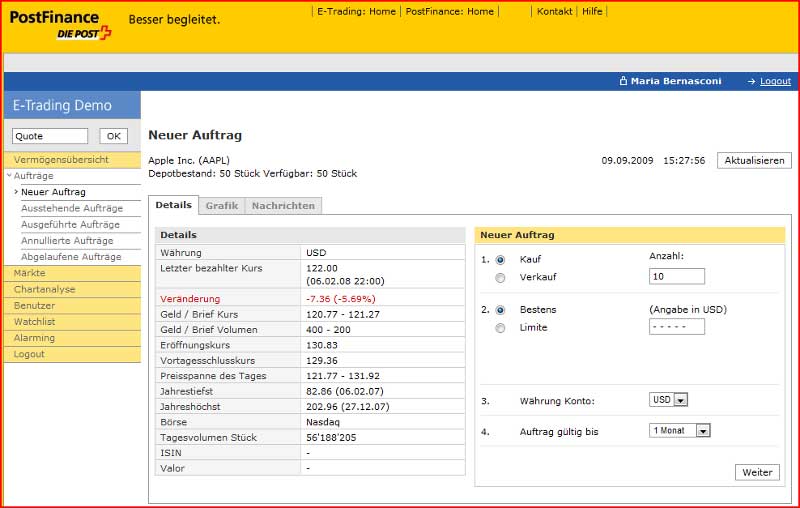
Keine Angaben über die Risiken beim Kauf eines Wertpapieres und auch nicht für das Gesamtrisiko des Portfolios. Es ist mir uner­klär­lich, war­um E‑Trading ein Werkzeug für die Chartanalyse anbie­tet und ander­seits ihren Onlinetrader über die Risiken sei­nes Portfolios im Dunkeln lässt.

Andere Handelsplattformen

Weiter habe ich auch die Demoversionen der Handelsplattform von Saxo Bank und Keytrade Bank kurz geprüft, auch dort kei­ne Angaben über Risiken. Anders bei der Rendite, die­se wird bei vie­len Onlinebrokern ausgewiesen.

Swissquote hat es, will dies aber teilweise bezahlt haben

Risikoangabe für Portfolio

Bei der Swissquote kann das Portfolio nach Value at Risk (VaR) aus­ge­wer­tet wer­den. Dieser wird für den aktu­el­len Tag, für eine Woche und einen Monat berech­net. Dasselbe gilt auch für den Value at Gain (VaG), mit die­sen Angaben kön­nen auch die Risiken für asym­me­tri­sche Anlagen dar­ge­stellt wer­den, was für vie­le struk­tu­rier­te Produkte sehr hilf­reich ist. Auch das Gesamtrisiko der Portfolios wird auf einer Skala von 1 bis 10 eingestuft.

swissquoterisiko

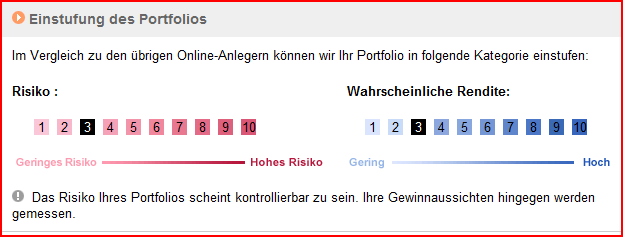
Bei Portfolios mit nur sym­me­tri­schen Anlagen wie bei­spiels­wei­se ETF’s, Aktien usw. wäre es wün­schens­wert, wenn die Risiken für ein Jahr aus­ge­wie­sen würden.

Risikoangaben beim Kauf

Der Equity- und Portfolio Analyzer von Swissquote schei­nen mei­nen Forderungen bezüg­lich der Risikoangaben beim Kauf einer Position auch zu erfül­len, lei­der konn­te ich die­se bei­den Werkzeuge noch nicht in Aktion sehen. Wobei Swissquote die­se Dienstleistung jähr­lich mit CHF 199.– in Rechnung stellt, eben­falls für Kunden mit einem Konto.

Onlinebroker ohne Risikozahl/en nicht akzeptabel

Für mich als Onlinetrader ist die­ser Zustand der feh­len­den Risikozahlen nicht akzep­ta­bel. Ich fra­ge mich, für was wir in der Schweiz eine eid­ge­nös­si­sche Finanzmarktaufsicht (fin­ma) haben. Diese ver­langt von ihr über­wach­ten Banken auch Risikozahlen, war­um hat der Privatanleger kein sol­ches Recht auf die­se Risikozahlen der Onlinebroker. Obliegt es nicht der fin­ma, den Kunden vor den Banken zu schützen?

Natürlich kön­nen die­se Risikowerte für vie­le Wertpapiere, irgend­wo im Internet gefun­den wer­den und das Risiko eines Portfolios kann der Trader selbst berech­nen. Nur gehö­ren Rendite und Risiko zusam­men und müs­sen ent­spre­chend auch von den Handelsplattformen berech­net und aus­ge­wie­sen werden.

Den Einwand, dass vie­le Trader die­se Zahlen sowie­so nicht ver­ste­hen wür­den, kann als Begründung auch nicht ange­führt wer­den. Falls ein Anleger die Risikowerte nicht ver­steht, kann er sich die­se von sei­nem Anbieter erläu­tern las­sen, mög­li­cher­wei­se lässt er sich die­se Dienstleistung gar bezahlen.

Eine Rendite über einer risi­ko­lo­sen Anlage umfasst auch ein Risiko, der Anleger hat Anrecht die­ses Risiko durch den Onlinebroker quan­ti­fi­ziert zu bekommen.

Rendite, Risiko, Korrelation und Diversifikation — Teil 3

Veröffentlicht am von

Berechnung der Korrelationen mit Excel

In die­sem Beitrag wer­de ich auf­zei­gen, wie Sie die Korrelation mit Excel selbst berech­nen kön­nen. An ein paar Praxisbeispielen wer­den wir sehen, war­um Korrelationen hilf­reich sein können.
Für das fol­gen­de Praxisbeispiel habe ich mir die Tageskurse eini­ger ETF’s sowie der Aktie Nestlé bei der SIX abge­holt. Auf Grund des UBS-ETF MSCI JAPAN (FDJPHU/ LU0136240974) hat mich noch die Korrelation zum Währungskurs JPY/CHF interessiert.

Wertpapier/Währung Standardabweichung 250 Tage
ZKB SILVER ETF  (ZSIL/ CH0029792717) 49.63%
ZKB GOLD ETF  (ZGLD/ CH0024391002) 28.84%
Xmtch (CH) SLI  (XMSLI/ CH0031768937) 38.36%
UBS-ETF MSCI JAPAN  (FDJPHU/ LU0136240974) 46.07%
NESTLE N  (NESN/ CH0038863350) 30.42%
DB X‑TR DAX  (XDAX/ LU0274211480) 47.06%
DB X‑TR SHORT DAX  (XSDX/ LU0292106241) 36.93%
JPY/CHF 17.13%

Die meis­ten die­ser Wertpapiere bzw. Währungskurs ste­hen in Zusammenhang mit mei­nem Portfolio, zudem woll­te ich mei­ne gefühls­mäs­si­gen Annahmen bezüg­lich Korrelationen zwi­schen den Wertpapieren überprüfen.

Korrelationen auf Tageskursen

Ich habe die Korrelationen für ein Jahr bzw. für 90-Tage auf den Tageskursen berechnet.

korr_jahr_b_tag

korr_90t_b_tag

Die 90-Tage-Korrelationen wur­den vom 22.04.2009 — 28.08.2009 berech­net, es sind also nicht 3 Monate, son­dern 90 Handelstage. Samstag, Sonntag und Feiertage gibt es kei­nen Börsenhandel, daher sind die­se Tage auch nicht in die Berechnung eingeflossen.

Korrelationen auf Wochenkurse

Ab einem Zeitraum von 6 Monaten emp­feh­le ich, die Wochenkurse zu neh­men und nicht die Tageskurse. Daher habe ich auch die Jahreskorrelationen auf der Basis von Wochenkursen berech­net, wobei ich den Freitag als Kurstag benutz­te. Im Dezember 2008 und Mai 2009 gibt es einen Zwei-Wochen-Sprung, dies soll­te das Ergebnis aber nicht stark beinträchtigen.

korr_jahr_b_woche

Tageskursen kön­nen manch­mal Extreme aus­wei­sen, was das Resultat der Korrelationen ein wenig ver­fälscht. Diese Extreme könn­ten sich inner­halb einer Woche wie­der nor­ma­li­sie­ren und daher sind Wochenkurse für die Erstellung von Korrelationen über einen län­ge­ren Zeitraum oft­mals die bes­se­re Wahl.

Korrelationen in der Praxis und meine gefühlsmässigen Annahmen

Wer die Kurse täg­lich oder wöchent­lich beob­ach­tet, wird wahr­schein­lich auto­ma­tisch gewis­se Korrelationen zwi­schen den Kursen der Wertpapiere fest­stel­len. Beispielsweise steigt der Ölpreis zur­zeit mit den Aktienindizes, dies ist nicht immer so. Noch im Jahr 2008, als der Ölpreis über UDS 100 lag, wie­sen die­se bei­den Assets eine nega­ti­ve Korrelation auf. Ich wer­de im Folgenden auf eini­ge Korrelationen die mein Portfolio beein­flus­sen eingehen.

Silber, Gold und Aktien

Es gibt eine star­ke Korrelation (>0.7) zwi­schen Gold und Silber. Ich hat­te aber in der letz­ten Zeit (90 Tage) das Gefühl, das der Silberpreis zuneh­mend auch mit den Aktienindizes kor­re­liert. Die 90-Tage-Korrelation scheint dies mit dem SLI und dem Dax zu bestä­ti­gen. Die auf ein Jahr hoch­ge­rech­ne­te Volatilität des Silbers war mit fast 50% weit­aus höher als die des Goldes mit nur zir­ka 29%.

gold_silber

Dass die Streuung beim Silber höher ist, lässt sich her­vor­ra­gend mit einem Punktdiagramm dar­stel­len. Im Oktober 2008 gab es beim Silber gar eine posi­ti­ve wie nega­ti­ve Rendite in Bereich von 10%.

Silber wird mehr als Gold in der Industrieproduktion ver­wen­det, daher schei­nen die höhe­re Korrelation zu den Aktien und höhe­re Volatilität gegen­über Gold nicht zu erstaunen.

Nestlé, SLI und Dax

Ich habe zur­zeit kei­nen direk­ten Aktientitel in mei­nem Portfolio, vor Kurzem habe ich mit Intel mei­ne letz­te Position ver­kauft. Trotzdem fin­de ich Nestlé eine mög­li­che Option für mein Portfolio, er ist mit einer Standardabweichung von zir­ka 30% weni­ger vola­til als der SLI mit cir­ca 38%. Zudem zahl­te Nestlé am 29.04.2009 eine Jahresdividende von CHF 1.40 pro Einheit, d.h. mehr als 3%. Die 90-Tage-Korrelation von Nestlé zum SLI beträgt nur 0.24, was die­sen Titel nebst der Dividendenzahlung zusätz­lich inter­es­sant macht. Dieser Titel könn­te defi­ni­tiv auch eine Bereicherung für ein rei­nes Anleihenportfolio sein.

UBS-ETF MSCI JAPAN und JPY/CHF

Zurzeit habe ich noch den UBS-ETF MSCI JAPAN (FDJPHU/ LU0136240974) in mei­nem Portfolio. Ich wer­de das Gefühl nicht los, das der stei­gen­de MSCI Japan ein­her­geht mit fal­len­dem Yen. Meine Annahme wird nur teil­wei­se von der 1‑Jahr-Wochenkurs-Korrelation bestätigt.

DB X‑TR DAX Dax und DB X‑TR DAX Short Dax

Wahrscheinlich erwar­ten Sie zwi­schen den bei­den ETF’s eine voll­stän­di­ge inver­se Korrelation. Die 1‑Jahr-Wochenkurs-Korrelation kommt mit ‑0.85 der ‑1 noch am nächs­ten. Ich stel­le mir vor, dass die Abweichung auf Grund des feh­len­den Volumens an der SIX zu Stande kommt bzw. die bei­den ETF’s den Dax kaum syn­chron exakt tra­cken. Diese Theorie wird durch die 1‑Jahr-Wochenkurs-Korrelation gestützt, damit wer­den die täg­li­chen Abweichungen zum Net Asset Value (NAV) teil­wei­se “geglät­tet”.

Anmerkung zu Excel

Damit die fol­gen­den Arbeitsmappen kor­rekt funk­tio­nie­ren, müs­sen Sie die Ausführung von Makros erlau­ben. Zuerst kön­nen Sie die­se ohne die Ausführung der Makros laden und den Quellencode der Makros im Microsoft Visual Basic [ALT]+[F11] prü­fen. Wie Sie oben sehen, wur­de Excel 2007 mit der “Bedingten Formatierung” erwei­tert. Eine sol­che Einfärbung einer Matrix ist nun “kin­der­leicht”.

Funktionen

KORREL(Matrix1;Matrix2)

Gibt den Korrelationskoeffizient einer zwei­di­men­sio­na­len Zufallsgrösse zurück, deren Werte in den Zellbereichen Matrix1 und Matrix2 ste­hen. Das Excelmakro CorrMatrix(Matrix) erleich­tert die Berechnung einer Matrix von Korrelationen, sie­he “Computing The Correlation Matrix – By Simon Benninga”. Dort kön­nen Sie auch ent­neh­men, wie eine sol­che Funktion in Excel ein­ge­ge­ben wird.

KOVAR(Matrix;Matrix2)

Diese Funktion gibt die Kovarianz zurück, den Mittelwert der für alle Datenpunktpaare gebil­de­ten Produkte der Abweichungen. Wie beim Korrelationskoeffizienten steht eine posi­ti­ve Kovarianz für eine posi­ti­ve linea­re Assoziation zwi­schen den Datenpunktpaar und umge­kehrt. Da der Wert der Kovarianz von den Einheiten der Datenpunktpaare abhängt, gibt es kei­nen “abso­lu­ten” Wert. Für den Anwender ist der Korrelationskoeffizient für die Beurteilung der Stärke der Assoziation weit­aus bes­ser geeig­net. Das Excelmakro VarCovar(Matrix) ermög­licht die Berechnung einer Matrix von Kovarianzen.

Arbeitsmappe für Excel 2007: Korr_Beispiel.xlsm 2007
Arbeitsmappe: Korr_Beispiel.xls

Rendite, Risiko, Korrelation und Diversifikation — Teil 2

Veröffentlicht am von

Im ers­ten Teil haben wir die Bedeutung der drei sta­tis­ti­schen Kenngrössen durch­schnitt­li­che Rendite (Mittelwert), die Streuung (Standardabweichung, Risiko, Volatilität) und Korrelation (Verhältnis zu ande­ren Wertpapieren) ken­nen gelernt. Wir wis­sen nun, dass die Rendite nur die hal­be Wahrheit ist und allei­ne nicht viel aus­sagt. Was zählt ist die risi­ko­ad­jus­tier­te Rendite oder eben die Rendite im Verhältnis zum Risiko.

Vorteil von Diversifikation

Anhand von zwei Portfolios kann der Vorteil der Diversifikation auf­ge­zeigt wer­den. In den bei­den fol­gen­den Portfolios wird eine Münze als Zufallsgenerator benutzt.

Portfolio mit einem Asset

Zuerst das Portfolio aus einem Asset, nen­nen wir dies Asset A.

Ergebnis Münzwurf Return
1 Kopf 30%
2 Zahl -10%

Eine simu­lier­te Serie wür­de eine Rendite von 1.3x0.9=1.17 für zwei Zeitperioden erge­ben, d. h. die Rendite beträgt zuerst 30% und danach folgt ein Verlust von 10%, daher die­se Multiplikation. Den am Anfang ein­ge­setz­ten Betrag kann mit 1.17 mul­ti­pli­ziert wer­den, um den Endbetrag zu berech­nen. Angenommen Sie hät­ten CHF 100 inves­tiert, dann hät­ten Sie nach zwei Zeitperioden CHF 117. Der Mittelwert (arith­me­ti­sche Mittel) ist 10% und die Standardabweichung beträgt 20%. Das geo­me­tri­sche Mittel beträgt 8.17%.

Geometrisches Mittel

Angenommen Sie besit­zen eine Aktie im ers­ten Jahr ver­dop­pelt sich die­se (100% Rendite) und im zwei­ten Jahr hal­biert sich der Wert (-50% Rendite), d. h. ein Verlust von 50%. Damit haben Sie in zwei Jahren kei­ne Rendite erzielt. Der Mittelwert ergibt aber (100%+(-50%))/2=25%, daher ist der Mittelwert bzw. durch­schnitt­li­che Rendite für die Berechnung der annua­li­sier­ten Renditen nicht brauch­bar. Mit dem geo­me­tri­schen Mittel √(2x0.5) — 1 = 0 erhält man die kor­rek­te Rendite. 100% wer­den als 2 abge­bil­det und die ‑50% als 0.5, damit ist das Resultat 1, da wir von 1 aus berech­ne­ten, wird am Schluss die 1 abgezogen.

Portfolio mit zwei Assets

Wir fügen dem Asset A ein Asset B hin­zu, die­ses hat die­sel­be Standardabweichung, Mittelwert usw. wie Asset A. Das Portfolio besteht je zu 50% aus Asset A bzw. Asset B.

Ergebnis Erster Münzwurf Zweiter Münzwurf Gesamtergebnis Berechnung Gesamtergebnis
1 Kopf Kopf +30% 0.5x1.3(A) + 0.5x1.3(B) = 1.3
2 Kopf Zahl +10% 0.5x1.3(A) + 0.5x0.9(B) = 1.1 
3 Zahl Kopf +10% 0.5x0.9(A) + 0.5x1.3(B) = 1.1
4 Zahl Zahl -10% 0.5x0.9(A) + 0.5x0.9(B) = 0.9

Da jedes der vier Ergebnisse der­sel­ben Wahrscheinlichkeit unter­liegt, ergibt sich einen Renditefaktor von 1.3x1.1x1.1x0.9 = 1.4157 für vier Zeitperioden. Der Mittelwert ist immer noch 10%, aber die Standardabweichung ist nur noch 14.14%, d. h. das Risiko des Portfolios wur­de redu­ziert. Zudem ist die annua­li­sier­te Rendite auf 9.08% ange­wach­sen. Wie ist dies möglich?

Wenn die Assets eines Depots nicht mit­ein­an­der kor­re­lie­ren, so ver­min­dert sich das Risiko bei mög­li­cher stei­gen­der Rendite. Das Ergebnis des ers­ten Münzenwurfes beein­flusst in kei­ner Weise den Zweiten, daher auch kei­ne Korrelation zwi­schen den bei­den Assets. Wären die bei­de Würfe per­fekt mit­ein­an­der kor­re­liert, so wür­de Ergebnis 2 und 3 nie ein­tre­ten und wir hät­ten die­sel­ben Renditen wie beim Portfolio mit einem Asset. Wären der zwei­te Wurf per­fekt mit dem Ersten invers kor­re­liert, so wür­de Ergebnis 1 und 4 nie ein­tre­ten, somit hät­ten wir ohne Risiko eine annua­li­sier­te Rendite von 10%. Leider wer­den wir nie lang­fris­tig eine voll­stän­di­ge inver­se Korrelation antref­fen — das wäre zu schön.

Arbeitsmappe: AssetAuAuBt.xls

Normalverteilung

Die Moderne Portfolio Theorie (MTP) wur­de 1952 in einem Aufsatz über “Portfolio Selection” von Harry Markowitz vor­ge­stellt. Markowitz hat­te die Annahme nor­mal­ver­teil­ter Renditen dabei nur als eine mög­li­che Voraussetzung für die Anwendbarkeit sei­ner Portfoliotheorie gese­hen. Vorausgesetzt wird von Markowitz, dass es sich bei der erwar­te­ten Rendite eines Wertpapieres um eine Zufallsgrösse han­delt, die inner­halb bestimm­ter Grenzen zufäl­lig schwankt. Die Normalverteilung mit der Standardabweichung σ (bzw. Varianz σ²) vom Erwartungswert μ wird wegen ihrer Einfachheit ger­ne in der Portfoliotheorie benutzt. Leider kann auf prak­tisch allen Finanzmärkten beob­ach­tet wer­den, dass die Wahrscheinlichkeit gros­ser Verluste oder auch Gewinne weit­aus höher ist, als es die Gauß’sche Glockenkurve vor­her­sagt. Ich möch­te die­se Problematik hier nicht wei­ter aus­füh­ren, lie­ber zei­ge ich bild­lich, war­um von einer Glockenkurve gespro­chen wird:

sp500_faz_net

Dieses Histogramm der Jahresrenditen des S&P 500 von 1825–2008 wur­de der FAZ.NET entnommen.

WARNUNG: Die his­to­ri­schen Erwartungswerte müs­sen sich aber kei­nes­wegs in der Zukunft, ins­be­son­de­re nicht in bestimm­ten Zeitperioden bestä­ti­gen. Dennoch ist die erwar­te Rendite bzw. erwar­te­te Risiko für eine län­ge­re Anlageperiode noch immer die Wahrscheinlichste.

Für die UBS habe ich die Häufigkeiten der Tagesrenditen vom 4.01.2005 — 14.08.2009 berech­net. Mit viel Fantasie ist auch hier eine Normalverteilung sicht­bar. Mit der Rendite von 31.66% gab es am 19.09.2008 einen Ausreiser im Gewinnbereich.

ubshaeufigkeit

Arbeitsmappe: ubsHaeufigkeit.xls

Rendite, Risiko, Korrelation und Diversifikation — Teil 1

Veröffentlicht am von

Vielleicht haben Sie auch einen Kollegen/in die Ihnen erzählt, sie habe gera­de “viel” Geld mit UBS-Aktien gemacht. Vielleicht hat die­se Person nur gera­de Aktien von 3 Unternehmen und behaup­tet, sie habe den gros­sen Durchblick bei Investitionen. Mit Simulationen kann ein­fach auf­ge­zeigt wer­den, dass wenig diver­si­fi­zier­te Portfolios fast in 70% aller Fälle hin­ter der Performance von gut diver­si­fi­zier­ten Portfolios zurückbleiben.

Ich wer­de daher eini­ge Einträge in die­sem Blog der Portfoliodiversifikation wid­men, dazu müs­sen zuerst ein wenig Wissen bezüg­lich Volatilität, Korrelationen usw. ver­mit­telt wer­den. Natürlich ist dies nicht für alle inter­es­sant und zudem muss man dabei sein Gehirn ein biss­chen bemü­hen. Viele Kleinanleger bewe­gen sich zufrie­den auf dem seich­ten Niveau der TV-Sendungen SF Börse. Gerade die Sendung SF Börse bewegt sich auf tie­fem Niveau. Hierzu ein Beispiel: Oftmals gegen die bei der Bekanntgabe von Unternehmensquartalszahlen des­sen Aktienkurs nach unten, dar­aus schliesst SF Börse, das die Anleger bes­se­re Zahlen erwar­tet haben. Dabei geht ver­ges­sen, dass der Aktienkurs die­ses Unternehmens viel­leicht schon weni­ge Tage vor­her in der Erwartung bes­se­rer Quartalszahlen “zu” stark gestie­gen war. Wahrscheinlich kennt SF Börse die Börsenweisheit nicht: “Kaufe das Gerücht, ver­kau­fe die Nachricht”. Anderseits ist es nicht erstaun­lich das sol­che Privatanleger im Jahre 2008 mehr als 40% ihres Vermögens an der Börse ver­spe­ku­liert haben.

Es ist rela­tiv leicht, die oben genann­te Angeber/in zu ent­zau­bern. Schon nur die Frage nach dem quan­ti­ta­ti­ven ein­ge­gan­ge­nen Risiko wird sie wahr­schein­lich nicht beant­wor­ten kön­nen. Es ist däm­lich nur von Renditen zu spre­chen, ohne dabei auch die damit ver­bun­de­nen Risiken zu erwähnen.

Risiko an realen Aktien bzw. ETF

Gerade vie­le Schweizer Privatanleger spe­ku­lie­ren mit UBS Aktien, dabei geht die hohe Volatilität die­ser Aktie ver­ges­sen. Scheinbar zieht die vie­le Medienpräsenz der UBS die klei­nen Privatanleger an. Manchmal kommt bei mir das Gefühl auf, der gesam­te Bundesrat arbei­te nur noch an den Problemen der UBS und die Schweizer Regierung sei der UBS hörig.

UBS Credit Suisse Group AG Nestlé AG DB X‑Trackers DJ Stoxx 600 Banks ETF
Kurs 14.08.2009 17.12 53.20 42.20 40.40
Performace 1 Monat 24.96% 7.87% 1.49% 27.46%
Performace lfd. Jahr 15.36% 86.67% 1.44% 52.73%
Performace 1 Jahr -21.25% 3.30% -14.95% -22.05%
Volatilität 30 Tage 43.66% 35.89% 20.79% 25.17%
Volatilität 1 Jahr 92.95% 87.07% 30.49% 61.85%

Dieser Tabelle vom 14.08.2009 kann ent­nom­men wer­den, dass die Volatilität bei der UBS-Aktie weit­aus am höchs­ten ist. Nur die Rendite der letz­ten 30 Tage belohnt die­ses ein­ge­gan­ge­ne Risiko. Wer schon viel Risiko ein­ge­hen will, hät­te bes­ser die Credit-Suisse gewählt, die Investition in UBS-Aktien war das Auslassen die­ser viel bes­se­ren Opportunität. Weniger ris­kant wäre die Investition in den DB X‑Trackers DJ Stoxx 600 Banks ETF als eine Direktinvestition in einen ein­zel­nen Banktitel. Wobei bei die­sem ETF das Währungsrisiko noch berück­sich­tigt wer­den müss­te und der Total Expense Ratio (TER) 0.3% beträgt.

Auch in die­sem vola­ti­len Marktumfeld bleibt das Risiko einer Nestlé Aktie gegen­über den Banktiteln in einem beschei­de­nen Rahmen.

Herkunft der historischen Daten

Bei OnVista kann unter der Rubrik Techn.-Analyse->Kennzahlen die Volatilität in % für die letz­ten 30 bzw. 250 Tage ein­ge­se­hen wer­den, wobei mit 250 Tagen ein Handelsjahr abge­deckt wird. Weitere freie Quellen für his­to­ri­sche Kurse von Schweizer Titeln:

Tabellenkalkulationsprogramm

Wahrscheinlich ken­nen vie­le Leser die­ses Blogs das Tabellenkalkulationsprogramm Microsoft Excel oder OpenOffice Calc. Ich wer­de mei­ne Berechnungen soweit als mög­lich mit die­sen Programmen durch­füh­ren und die Arbeitsmappen bereitstellen.

Risiko und Volatilität

Volatilität wird in der Finanzwelt als eine der bedeu­tends­ten Risikokennzahlen ange­se­hen. Allerdings ist die­se Risikokennziffer ein zwei­schnei­di­ges Schwert. Gehen wir bei­spiels­wei­se von einem simp­len Aktieninvestment aus, so gibt Volatilität kei­ne Auskunft dar­über, ob die Aktie stei­gen oder fal­len wird. Vielmehr bedeu­tet eine gestie­ge­ne Volatilität zum einen, dass die Wahrscheinlichkeit von gros­sen Kursverlusten gestie­gen ist, zum ande­ren aber auch, dass es wahr­schein­li­cher gewor­den ist, dass die Aktie star­ke Kursgewinne ver­zeich­nen wird. Demzufolge ist es nun weni­ger wahr­schein­lich, dass die Aktie dicht um das aktu­el­le Niveau schwankt. Volatilität ist ein Mass für die Schwankungsintensität eines Aktienkurses, die häu­fig als die annua­li­sier­te Standardabweichung der Tagesrenditen dar­ge­stellt wird. [1]

Fast alle Fonds-Ratingagenturen lis­ten die Standardabweichung in ihren Berichten auf. Normalerweise wer­den die Standardabweichungen der letz­ten drei, fünf und zehn Jahre auf­ge­führt. Wenn es nur Zahlen für ein oder zwei Jahre gibt, kann die Standardabweichung auf Grund der vier­tel­jähr­li­chen Renditen mit 2 (√4) bzw. der monat­li­chen Renditen mit 3.46 (√12) mul­ti­pli­ziert wer­den. Die Standardabweichungen ver­schie­de­ner Asset-Klassen sehen in der Regel so aus:

Asset-Klasse Standardabweichung
Geldmarkt 2–3%
Kurzlaufende Anleihen 3–5%
Langlaufende Anleihen 6–8%
Konservative Aktien 10–14%
Spekulative Aktien 15–25%
Emeringmarket Aktien 25–35%

Immer wenn Ihnen Ihr Bankberater ver­sucht eine bestimm­te Investition schmack­haft zu machen, fra­gen Sie ihn nach der Standardabweichung oder einem ande­ren übli­chen Risikomass. Lassen Sie sich die­ses Risikomass aus­führ­lich erklä­ren, wenn der Berater dies nicht kann, so soll­ten Sie die­sen umge­hend durch eine kom­pe­ten­te­re Person erset­zen. Bei der Standardabweichung soll­ten Ihrem Berater die fol­gen­den Aussagen bekannt sein.

In der Mathematik wird die Standardabweichung einer Zufallsvariablen häu­fig mit dem grie­chi­schen Buchstaben σ (Sigma) bezeich­net und ist in der Regel wie folgt definiert:
standardabweichungformel

Ri: Rendite mit Anzahl i; n: Periodenanzahl; x: Anlagebeginn; y: Anlageende

Bei Wikipedia kön­nen Sie die Formel anhand eines Beispieles in Aktion sehen. Wichtig ist die sind die Häufigkeiten der Realisationen in den ver­schie­de­nen Intervallen:

  • 68.27% aller Realisationen haben eine Abweichung von höchs­tens einer Standardabweichung vom Mittelwert.
  • 95.45% aller Realisationen haben eine Abweichung von höchs­tens 2 Standardabweichungen vom Mittelwert.
  • 99.73% aller Realisationen haben eine Abweichung von höchs­tens 3 Standardabweichungen vom Mittelwert.

Volatilität bei Jahresrenditen anhand eines Beispieles

Datum Jahres-
endkurse		 Rendite p.a. Log. Rendite Mittelwert
Standard-
abweichung		 Intervall 68.27
Intervall 95.45
Intervall 99.73
fol­gen­des Jahr
1998 31.13
1999 31.72 1.89% 1.8775% 1.8775%
2000 39.03 23.04% 20.7383% 11.3079%
13.34%		 [-2.03%,24.64%]
[-15.37%,37.98%]
[-28.70%,51.32%]
2001 37.09 -4.97% -5.0983% 5.8392%
13.37%		 [-7.53%,19.21%]
[-20.89%,32.57%]
[-34.26%,45.94%]
2002 29.75 -19.78% -22.0518% -1.1336%
17.71%		 [-18.84%,16.57%]
[-36.55%,34.28%]
[-54.26%,51.99%]
2003 37.49 26.01% 23.1245% 3.7180%
18.78%		 [-15.07%,22.50%]
[-33.85%,41.29%]
[-52.64%,60.07%]
2004 42.21 12.59% 11.8583% 5.0748%
17.13%		 [-12.05%,22.20%]
[-29.18%,39.33%]
[-46.31%,56.46%]
2005 55.38 31.20% 27.1561% 8.2292%
17.72%		 [-9.49%,25.95%]
[-27.22%,43.68%]
[-44.94%,61.40%]
2006 65.86 18.92% 17.3313% 9.3670%
16.72%		 [-7.35%,26.09%]
[-24.08%,42.81%]
[-40.80%,59.53%]
2007 46.60 -29.24% -34.5931% 4.4825%
21.43%		 [-16.95%,25.92%]
[-38.38%,47.35%]
[-59.82%,68.78%]
2008 14.85 -68.13% -114.3601% -7.4017%
42.67%		 [-50.07%,35.27%]
[-92.74%,77.94%]
[-135.41%,120.61%]

Arbeitsmappe: UbsStandardAbweichungRendite.xls

Ich habe auf Grund der Jahresrenditen der UBS-Aktie, die Standardabweichungen der letz­ten 8 Jahre (2000–2008) pro Jahr berech­net. Natürlich kann die Standardabweichung, die nur auf weni­gen Werten berech­net wur­de, nicht aus­sa­ge­kräf­ti­ge Resultate für die ers­ten Jahre lie­fern. In bei­den Finanzkrisenjahren 2007 und 2008 sind Erwartungen und Realität voll­stän­dig aus­ein­an­der gelau­fen. Noch bis Ende 2006 war die Standardabweichung um die 17% über Jahre hin­weg sehr sta­bil, erst der Verlust im 2007 liess die Standardabweichung über 21% anstei­gen. Die immense Kurseinbusse von über 68% im Jahre 2008 soll­te gemäss log­arith­mier­ten Normalverteilung nur alle 740 (es ist weit mehr als 3 Standardabweichungen, daher auch mehr als 740 Jahre — aber so genau wol­len wir es auch nicht wis­sen) Jahre mög­lich sein, das zeigt die Grenzen die­ses sta­tis­ti­schen Modells für Aktienkurse.

Die Spalte “Intervall 68.27” bedeu­tet das nur alle 6.3 Jahre ein Verlust bzw. Gewinn von mehr als das im ange­ge­ben Intervalls zu rech­nen ist. Beispielsweise bewegt sich das Jahr 2006 bei einem Gewinn von 18.92% im erwar­te­ten Intervall [-9.49%, 25.95%].

Die Spalte “Intervall 95.45” bedeu­tet das nur alle 44 Jahre ein Verlust bzw. Gewinn von mehr als das im ange­ge­ben Intervalls zu rech­nen ist. Das Jahr 2005 endet im die­sem Intervall [-29.18%, 39.33%].

Die Spalte “Intervall 99.73* bedeu­tet, dass nur all 740 Jahre ein Verlust bzw. Gewinn von mehr als das im ange­ge­ben Intervalls zu erwar­ten ist. Der Verlust von 29% in Jahre 2007 bewegt sich in die­sem Intervall [-40.80%, 59.53%].

Korrelationen

Wird ein Vermögen auf ver­schie­de­ne Asset-Klassen ver­teilt, hängt das Risiko des Portfolios weni­ger von der Volatilität der ein­zel­nen Anlage als vom Zusammenhang zwi­schen den ver­schie­de­nen Asset-Klassen ab. Mit der Diversifikation wird ver­sucht, bei einem vor­ge­ge­be­nen Risiko die maxi­ma­le Rendite zu erzie­len, bzw. für eine anvi­sier­te Rendite das geringst­mög­li­che Risiko einzugehen.

Die gegen­sei­ti­ge Abhängigkeit von zwei Anlageformen wird mit dem sta­tis­ti­schen Mass der Korrelation gemes­sen. Dieses Mass liegt defi­ni­ti­ons­ge­mäss zwi­schen +1 und ‑1, wobei eine Korrelation von 1 bedeu­tet, dass die Renditen zwei­er Anlagen in einem per­fekt posi­ti­ven Zusammenhang ste­hen. Eine sol­che Kombination von Anlagen bie­tet kei­ne Diversifikation. Ein Korrelationskoeffizient von ‑1 heisst, dass sich die bei­den Anlagen genau gegen­läu­fig entwickeln.

Investoren müs­sen akzep­tie­ren, dass Korrelationen nicht in Stein gemeis­selt sind, dies kann der fol­gen­den Tabelle ent­nom­men wer­den. Hier sind die Jahres-Korrelationen von 1973 bis 2008 eini­ger Assetklassen zum S&P 500 aufgeführt.

Asset-Klasse Durchschnitt Maximum Minimum
Nicht U.S. Aktien 0.54 0.96 -0.41
U.S. Bonds 0.20 0.86 -0.85
Commodities 0.01 0.95 -0.79
Real Estate 0.55 0.97 -0.30

Gerade wenn die Märkte sich in “Stresssituationen” befin­den, ten­die­ren die Korrelationen gegen die 1, d.h. alle Asset-Klassen tau­chen bei­spiels­wei­se zusam­men ab.

Bei Goldman Sachs kann eine Korrelationsmatrix ein­ge­se­hen werden.

korrelation200906_goldmangross
Quelle: Goldman Sachs — Korrelationsmatrix, Juni 2009

Diese Matrix zeigt die Korrelationen der Renditen von ver­schie­de­nen Anlageklassen. Dabei sind im lin­ken Dreieck (unter­halb der schwar­zen Linie) die Fünfjahreskorrelationen dar­ge­stellt. Im rech­ten Dreieck befin­den sich die Einjahreskorrelationen.

Bei der Asset-Klasse Aktien haben die Indizes eine hohe Korrelation zuein­an­der. Bei eini­gen Rohstoffen Indizes ist die Korrelation seit einem Jahr deut­lich höher als bei den Fünfjahreskorrelationen, wobei Gold oder der S&P GSCI Precious Metals ER (Edelmetall) eine gute Diversifikation zu Aktien ist. Staatsanleihen haben gegen­über den Aktien gar eine nega­ti­ve Korrelation. Auf die Spekulation mit Devisen möch­te ich hier nicht wei­ter eingehen.

Im Payoff maga­zi­ne vom 07/2009 habe ich eine wei­te­re Korrelationsmatrix gefun­den. Dabei ent­spre­chen alle Werte im lin­ken unte­ren Dreieck der Korrelation der letz­ten 52 Wochen (auf wöchent­li­cher Basis gemessen).

korrelation200907_payoff

Der USD/CHF Wechselkurs und der Goldpreis wei­sen eine nega­ti­ve Korrelation von ‑0.46 auf, d.h. wenn der USD gegen­über den CHF schwä­cher wird, dann steigt der Goldpreis. Mit Gold kann daher der USD teil­wei­se abge­si­chert werden.

Anmerkung Korrelationen

Auch wenn eine voll­stän­di­ge Korrelation zwi­schen zwei Titeln besteht, kann die Rendite unter­schied­lich hoch aus­fal­len. Im fol­gen­den Beispiel wur­de die Rendite von Grafiosch aus der Rendite von ABC AG mul­ti­pli­ziert mit 0.5 + 3% berech­net. Weil die zwei Renditen line­ar sind, ergibt dies eine voll­stän­di­ge Korrelation.

Unterschiedliche Renditen und trotz­dem vollständig
korreliert
Jahr Rendite ABC AG Rendite Grafiosch
2000 23.05% 14.52%
2001 -4.97% 0.51%
2002 -19.79% -6.89%
2003 26.02% 16.01%
2004 12.59% 9.30%
2005 31.20% 18.60%
2006 18.92% 12.46%
2007 -29.24% -11.62%
2008 -68.13% -31.07%
Korrelation = 1.0

korrelationlinear

Arbeitsmappe: GrafioschABCLinearKorr.xls

Diversifikation

Auch ein rei­nes Aktienportfolio soll­te breit diver­si­fi­ziert sein. Modellrechnungen haben erge­ben, dass ein glo­ba­les diver­si­fi­zier­tes Portfolio über 100 ver­schie­de­ne Titel ent­hal­ten müss­te. Bei einem regio­na­len Portfolio genü­gen oft schon 20 Titel. Daraus wird ersicht­lich, dass die meis­ten Privatanleger für eine brei­te Diversifikation ihres Portfolios gar nicht ein­zel­ne Aktientitel kau­fen soll­ten, die Transaktionskosten und der Aufwand wären viel zu hoch. Mit den bei­den ETF auf dem MSCI World und dem MSCI Emerging Markets hat der Privatanleger eine güns­ti­ge Möglichkeit sein Aktienportfolio zu diversifizieren.

emergingworldkorr

Diese Korrelation kön­nen bei db x‑trackers unter Tools–>Korrelationsmatrix für 1, 3 und 5 Jahre ein­ge­se­hen wer­den. Die Korrelation zwi­schen dem MSCI EMERGING MARKETS TRN INDEX und dem MSCI WORLD TRN INDEX ist mit 0.81 rela­tiv hoch. Bei MSCI World gefällt mir die star­ke Gewichtung der USA mit zir­ka 50% und Grossbritannien mit zir­ka 10% nicht unbedingt.

In einem wei­te­ren Eintrag wer­de ich ver­mehrt über die Korrelationen und Portfoliotheorie schreiben…

[1] Volatilitäts-Kompass

Wo welchen ETF kaufen?

Veröffentlicht am von

Oftmals wird der­sel­be ETF an ver­schie­de­nen Börsen gehan­delt. Beispielsweise der iShares Dow Jones Euro STOXX 50 (IE0008471009). Er kann an der SIX Swiss Exchange, London Stock Exchange, Borsa Italiana usw. gekauft wer­den. In der Schweiz ist die Handelswährung der CHF, in London der GBP und in Italien die Basiswährung EUR.

Wahl eines ETFs für einen gewälten Index

Die Wahl der Handelsbörse für einen ETF ist nicht so wich­tig, die­se wird zum gröss­ten Teil durch die Courtagen des Onlinebrokers und der bevor­zug­ten Handelswährung bestimmt. Einige Schweizer Onlinebroker berech­nen ihren Kunden höhe­re Courtagen an den aus­län­di­schen Handelsbörsen. Wichtiger kann die Wahl des Produktanbieters sein, ETFs für den Dow Jones EURO STOXX 50 bei­spiels­wei­se gibt es von meh­re­ren Anbietern.

Name ISIN Handels- wäh­rung Verwaltungs- geb??ühr Aktuell Umsatz 12.6.2009 Dividende Fonds- ver­mö­gen Bemerkung
db x‑trackers DJ EURO STOXX 50 ETF LU0274211217 CHF 0.15% 39.75 1’697’787 unre­gel­mäs­sig 1.3 Mrd. Günstig und hat guten Umsatz, aber in CHF
iShares DJ EURO STOXX 50 IE0008471009 CHF 0.35% 38.86 145’339 Vierteljährlich 3.6 Mrd. Zu teu­er und in CHF
iShares DJ EURO STOXX 50 (DE) DE0005933956 EUR 0.15% 25.83 43’687 Vierteljährlich 3.9 Mrd. Günstig aber an der SIX zu wenig gehan­delt — hoher  Umsatz bei Xetra
Lyxor ETF DJ Euro Stoxx 50 FR0007054358 EUR 0.25% 25.94 170’672 unre­gel­mäs­sig 4.6 Mrd. Gebühr eher hoch aber an der SIX die Alternative
UBS-ETF DJ EURO STOXX 50 LU0136234068 EUR 0.30% 25.92 488’710 2x pro Jahr 0.5 Mrd. Gebühr teu­er
UBS-ETF DJ EURO STOXX 50℠ LU0136234068 CHF 0.30% 39.19 44’089 2x pro Jahr 0.5 Mrd. Gebühr teu­er
UBS-ETF DJ EURO STOXX 50 I LU0155367302 EUR 0.10% 25924.50 103’585 2x pro Jahr 0.4 Mrd. Die Produkt ist auf insti­tu­tio­nel­le und ver­mö­gen­de Privatinvestoren ausgerichtet.

Die Auswahl des Produkts hängt von eini­gen Kriterien ab, wie bei­spiels­wei­se von Liquidität, Verwaltungsgebühren, Fremdwährung, Index-Replikation usw.:

  • Liquidität und Spread: Der Designated Sponsors der ETFs, muss die Liquidität des Indexfonds sicher­stel­len, daher wird es immer einen An- und Verkaufspreis geben. Die Differenz zwi­schen den bei­den Kursen, d.h. der Spread kann bei vola­ti­len Börsen durch­aus eini­ge weni­ge Prozente betra­gen. Grundsätzlich sind Produkte und Börsen zu bevor­zu­gen, wo der ETF hohe Umsätze erzielt und damit der Spread in der Regel gerin­ger ist.
  • Verwaltungsgebühren: In den USA sind ETFs sehr beliebt und die Umsätze der bekann­ten Indizes im Vergleich mit Europa sehr hoch. Beispielsweise ist die Verwaltungsgebühren des S&P 500 SPDR (US78462F1030) mit 0.1% deut­lich güns­ti­ger als die des iShares S&P 500 (IE0031442068) mit 0.4%. Anderseits wer­den bei der Auszahlung von Dividenden eines US-ETF, auto­ma­tisch 30% für die Steuer in Abzug gebracht. Die Hälfte die­ses Steuerrückbehaltes kön­nen zurück­ge­for­dert wer­den, d.h. 15% der Dividenden kas­siert die USA. Wenn bei­spiels­wei­se der SPDR S&P 500 eine Dividende von 2% und mehr aus­zahlt, so geht der Gebührenvorteil 0.3% (2x0.15) gegen­über dem iShares S&P 500 auf Grund der US-Steuern ver­lo­ren. In die­sem Fall ist der iShares S&P 500 die bes­se­re Wahl.
  • Fremdwährung: Die gän­gi­gen Fremdwährungen der an SIX Swiss Exchange gehan­del­ten ETFs sind CHF, EUR GBP, JPY und USD. Vielleicht möch­te jemand kein JPY-Konto bei sei­nem Onlinebroker eröff­nen, daher wird er mög­li­cher­wei­se den UBS-ETF MSCI Japan A (LU0136240974) der in CHF gehan­delt wird bevor­zu­gen. Damit kann der Währungstausch durch den Anleger ver­mie­den wer­den, die­ser CHF -> JPY -> CHF wür­de sicher­lich 2% Performance kosten.
  • Index-Replikation: Einige ETF-Anbieter set­zen stark auf syn­the­ti­sche Nachbildung des Index. Damit geht der ETF ein Gegenpartrisiko bis zu maxi­mal 10% des Nettoinventarwerts ein. Einige Anleger wol­len die­ses Gegenpartrisiko mög­lichst ver­mei­den und wer­den daher Produkte mit voll­stän­di­ger Indexnachbildung bevorzugen. 

Onlinebroker und ETF-Handel

Die Schweizer Onlinebroker haben alle ihre Einschränkungen. Bei einer UBS und die Credit Suisse sind die Courtagen für durch­schnitt­lich ver­mö­gen­de Anleger viel zu hoch. Daher wer­den Alternativen wie Keytrade, Migros Bank und Swissquote usw. die bes­se­ren Alternativen, lei­der haben auch die­se Broker ihre Unzugänglichkeiten:

Onlinebroker Courtage Bemerkung
Migros Bank Pauschalbreis CHF 40.00 Ab Aufträge von CHF 30’000 ist sie güns­ti­ger als die meis­ten ande­ren Schweizer Onlinebroker.
E‑Trading Postfinance Keine Vergünstigung für ETFs Kontos sind begrenzt auf die Währungen CHF, USD und EUR.
Swissquote Pauschalpreis CHF/EUR/USD 9.00 Der Pauschalpreis gilt nur für die SIX Swiss Exchange. Für an den US-Börsen gehan­del­ten ETF, ist Echtzeithandel nicht mög­lich, Aufträge wer­den frü­hes­tens den nächs­ten Tag ent­ge­gen genommen.

Wahrscheinlich wäh­ren die aus­län­di­sche Onlinebroker die bes­se­re Wahl…

Anleihen in der Praxis

Veröffentlicht am von

Seit zir­ka 3.5 Jahren neh­me ich aktiv am Wertpapierhandel teil. Am 14.11.2006 kau­fe ich zum Kurs von EUR 98.00 mei­ne ers­te Anleihe (auch Obligation oder eng­lisch Bond genannt), 3.125 RABOBK 10/EE (XS0210106695). Diese wer­de ich wahr­schein­lich bis zum Verfallsdatum halten.

Ich schrei­be hier über mei­ne Erfahrungen mit Anleihen und Obligationenfonds, in einem zukünf­ti­gen Eintrag wer­de ich ver­mehrt in die Theorie von Anleihen ein­ge­hen. Scheinbar sind Anleihen eine „lang­wei­li­ge“ Asset Klasse die nicht viel Wissen benö­tigt, ich kann Ihnen ver­si­chern, dass dies nicht zutrifft. Sie wer­den sehen was ich schon für Fehler gemacht habe und dar­aus lernte.

Wer gut essen will, kauf Aktien. Wer gut schla­fen will, kauf Obligationen. Diese Börsenweisheit trifft nicht immer zu, auch Obligationen kön­nen hohen Kursschwankungen unter­lie­gen. Zudem sind hohe Teilverluste oder gar Totalverluste mög­lich, als Beispiel nen­ne ich hier die Anleihe 7.25 GM 13 /EE (XS0171942757) von General Motors:

725gm_13

Eine sol­che Anleihe hät­te der Anleger lie­ber nicht im Portfolio!

Langfristig gese­hen ver­spre­chen Frankenobligationen nur 4.47% Rendite; das zei­gen Statistiken der Genfer Privatbank Pictet & Cie für den Zeitraum von 1926 – 2008. In der­sel­ben Periode erreich­ten die Aktien eine Jahresperformance von 7.6%, sie­he “Die Performance von Aktien und Obligationen in der Schweiz”.

Meine Erfahrungen

Obligationenfonds

Meine ers­ten Börsentransaktionen wickel­te ich bei der Postfinance ab. Zuerst kauf­te ich mir im Jahr 2006 eini­ge Aktientitel und spä­ter im Jahr auch Obligationen. Im Dezember 2006 dach­te ich mir, es wäre gut auch eini­ge High Yield Obligationen zu besit­zen. Diese woll­te ich aber nicht selbst über­wa­chen, son­dern den Anlageprofis über­las­sen. Daher kauf­te ich am 27.11.2006 bei der UBS den UBS (CH) Bond High Yield (CH0002775242) zum Kurs von 83.34, dabei muss­te ich eine Ausgabekommission von 1.35% bezahlen.

Im 2007 betrug die Performance nach Abzug von Gebühren ‑1.8% und im 2009 gar ‑9.4%. Die pau­scha­le Verwaltungskommission beträgt 1.02% p.a..

Noch im Dezember 2006 wur­de der Fonds in UBS Key Selection CHF Bonds unbe­nannt. Damit waren mein Ziel, der Investition in High Yield Bonds ver­fehlt wor­den. Das Portfolio die­ses Fonds ent­hält nur zir­ka 6% High Yield Bonds. Am 15.08.2008 habe ich die­sen mit einem Verlust von 5.82% exklu­siv Steuerbelastung ver­kauft. Der Verkauf ver­ur­sach­te kei­ne zusätz­li­chen Kosten.

ubskeyselection

Im Chart ist ersicht­lich, dass der Kurs nach Zinszahlung um die aus­be­zahl­ten Prozente ein­bre­chen kann.

Wer nicht ein­zel­ne Firmenanleihen han­deln will, kann dies bei­spiels­wei­se mit dem iShares Euro Corporate Bonds (CHF) ETF, ein breit diver­si­fi­zier­tes Anleihenportfolio kau­fen. Bei die­sem ETF betra­gen die jähr­li­chen Gebühren 0.2%, d.h. er ist 5‑mal güns­ti­ger als der UBS Key Selection CHF.

Rating (Bonität)

Ratings von AAA bis BBB wer­den als Investment-Grade bezeich­net und kön­nen unter ande­rem an der SIX Swiss Exchange gehan­delt wer­den. Als Sub-Investemtn-Grade, Junk oder High Yield wer­den die Ratings von BB bis D genannt.

Rating Risiko
AAA Hohe Kreditqualität, höchs­te Bonitätsstufe
AA Hohe Kreditqualität, Risiko aber etwas höher als bei AAA
A Gute Kreditqualität ist in wid­ri­gen Konjunkturlagen im stär­ke­ren Masse aus­ge­setzt, als höher ein­ge­stuf­te Emittenten
BBB Ausreichende Kreditqualität, mit höhe­rem Kurs- und Ausfallrisiko als Emittenten mit höhe­rem Rating 
BB Geringe Risikoqualität
B Hohes Ausfallrisiko, kann jedoch aktu­ell sei­nen Verpflichtungen nachkommen
CCC Erhebliches Ausfallrisiko, bei ungüns­ti­gen kon­junk­tu­rel­len oder wirt­schaft­li­chen Bedingungen, wird der Emittent in Verzug geraten
CC Ausfallwahrscheinlichkeit sehr hoch
C Möglicherweise schon Konkurs, leis­ten jedoch wei­ter­hin Zahlungen auf die­se Verbindlichkeit
D In Verzug mit Zahlungsverbindlichkeiten und hat Konkurs beantragt

Fremdwährungsanleihe

Am 20.12.2006 kauf­te ich den 3.75 Swedish Covert Bond 08, damals war der Wechselkurs EUR/CHF 1.61. Ich hielt die­se Anleihe bis zum Verfall am 20.11.2008. Wenn eine Anleihe bis zum Verfall gehal­ten wird, so ent­fällt natür­lich die Courtage und eidg. Umsatzabgabe von 0.15%. Am 20.11.2008 war der Kurs EUR/CHF 1.52, damit habe ich einen Währungsverlust von zir­ka 5.5% erlitten.

Rechnet man die Währungsverluste, Courtage, Depotgebühren usw. zusam­men, so fällt die Rendite vor Steuer unter 1.5% zusam­men, dabei habe ich nach dem Verfall der Anleihe den Währungsaustausch vermieden.

Auch wenn höhe­re Zinsen von Fremdwährungsanleihen oft­mals sehr ver­lo­ckend sind, ist dies aus der CHF-Sicht mit hohen Fremdwährungsrisiken verbunden.

Meine Strategie 2008

Seit ich bei der Migros Bank ein Depot habe und die­se eine Ticket Fee von CHF 40.00 anbie­tet, ist es durch­aus eine Option eine Anleihe nicht mehr bis zu ihrem Verfall zu hal­ten. Angenommen Sie hät­ten am 15.10.2007 fol­gen­de Anleihe mit dem m‑bancnet bei der SIX gekauft:

CHF 30,000 3 1/8 % OBL COOP  2007–28.9.10 VALOR
003.418.237.5 ZU 99.95 %		    
    KURSWERT CHF 29,985.00
    ZINS CHF 52.10
    STEUERN, MARKTGEBUEHREN, FREMDE SPESEN ETC. CHF 3.00
    BRUTTO CHF 30,040.10
    COURTAGE CHF 40.00
    EIDG. UMSATZABGABE + SWX/EBK-GEBUEHR CHF 24.05


Wie man sieht, kann man bei der Migros auch Coop kaufen.

Der letz­te Zinstermin bzw. Liberierung von die­ser Anleihe war der 28.9.2007, die auf­ge­lau­fe­nen Zinsen von CHF 51.10 bis zum 15.10.2007 müs­sen dem Verkäufer bezah­len. Es muss kei­ne Verrechnungssteuer von 35% bezahlt wer­den, die­se wird erst am 29.9.2008 auto­ma­tisch mit der Jahreszinszahlung von CHF 937.50 in Abzug gebracht. Auf aus­län­di­sche Anleihen wird kei­ne Verrechnungssteuer erho­ben. Wenn Sie die Anleihe kurz vor dem Zinstermin ver­kau­fen, dann kann der auf­ge­lau­fe­ne Marchzins als steu­er­frei­er Kapitalgewinn kas­siert werden.

Für die Steueroptimierung ist es bes­ser Anleihen unter pari zu kau­fen, d.h. unter 100% des Nominalwertes. Wenn der Rückzahlungskurs bei Laufzeitende bzw. bei einem Verkauf zu pari oder über pari geschieht, kann die Differenz zwi­schen Kaufkurs und Verkaufskurs/Rückzahlungskurs als ein­kom­mens­steu­er­frei­er Kapitalgewinn ver­bucht werden.

Wie kaufe ich zurzeit meine Anleihen?

Seit Oktober 2008 wie­der­ho­le ich fol­gen­des Szenario des Öfteren um die Mittagszeit oder spä­ter an der SIX mit der Anleihensuche. Wie oben beschrie­ben sind Fremdwährungsanleihen pro­blem­be­haf­tet, daher erfolgt die Sucheinstellung für CHF-Anleihe. Als Preis wird maxi­mal 100% gewählt, wegen Steueroptimierung und als Laufzeit wäh­le ich zwi­schen 1–7 oder 1–10 Jahre.

bondselectionsix

Das Resultat öff­ne ich als Excel-Sheet und mit dem Datenfilter wer­den nur die­se ange­zeigt, wel­che einen Umsatz an die­sem Tag hat­ten. Ich kau­fe nur Anleihen, die mehr oder weni­ger täg­lich gehan­delt werden.

excelbondselection

Danach suche ich Anleihen, des­sen Kurs an die­sem Tag gesun­ken ist und mög­lichst eine hohe Rendite auf­weist. Zudem soll­te das letz­te Zinsdatum mög­lichst nicht mehr als 3 Monate zurück­lie­gen, wobei dies auch sehr stark abhängt, wie lan­ge ich geden­ke, die Anleihe zu hal­ten. Zurzeit gehe ich davon aus, dass ich die Anleihe nicht bis zum Verfallsdatum hal­ten wer­de. Bei der Auswahl der Anleihe den­ke ich dar­an, wie sich die­se nega­tiv auf mei­ne Steuerrechnung aus­wir­ken könnte.

Andere wichtige Merkmale einer Anleihe

Coupon (Zinscoupon): Periodische Zinszahlung in Prozent des Nominalwerts.

Rendite (Rendite auf Verfall, Yield to matu­ri­ty): Die Rendite auf Verfall ist im Gegensatz zu der Angabe des Coupon rela­tiv exakt, weil neben dem Jahreszins auch die Restlaufzeit und die Kursdifferenz zum Nennwert in die Berechnung ein­fliesst. Wenn der Zinscoupon 5% beträgt und der Kurs bei 103 liegt wird die Rendite auf Verfall klei­ner aus­fal­len als die 5%, anders wenn der Kurs unter pari liegt, dann wird die Höhe der Rendite grös­ser als 5% sein. Dadurch wird klar das der intel­li­gen­te Investor mit die­ser Kennzahl bei der Auswahl der Anleihe arbei­tet und nicht mit dem Zinscoupon.

Duration: Diese zeigt an, wie stark eine Anleihe oder ein Portfolio auf Zinsänderungen reagiert. Anders aus­ge­drückt, schätzt die Duration um vie­le Prozentpunkte sich der Kurs ändern wür­de, wenn sich die Zinsen um 1% bewe­gen. Angenommen der Zins steigt um 1%, dann wür­de eine Anleihe mit einer Duration von 2, einen erwar­ten Kursrückgang von 2% haben. Weitere Erläuterungen sie­he Bewertung von Anleihen.

Restlaufzeit in Jahren: Anzahl Jahre vom jet­zi­gen Datum bis zur Rückzahlung der Anleihe.

Bei der SIX Swiss Exchange gibt es einen Anleihenrechner, damit kön­nen die wich­ti­gen Kennzahlen berech­net werden.

Einige Beispiele

Ich gehe jetzt hier auf eini­ge Beispiele von Anleihen ein, dabei spielt das Verfalldatum kei­ne Rolle. Viele Unternehmensanleihen sind seit den Tiefs vom März 2009 wie­der hef­tig gestie­gen. Es gibt aber durch­aus noch Staats- oder Unternehmensanleihen mit einer Rendite von 4% und mehr. Die meis­ten Anleihen mit hoher Rendite sind vom aus­län­di­schen Finanzsektor oder Staatsanleihen von Staaten wie Ungarn, Mexiko usw..

Aktuel- ler Kurs Coupon Emittent Rating Rendite Duration Rest- lauf­zeit in Jahren Verfall Kurs Differenz Meine Bemerkung
45.25 2.88% American International Group BBB 20.88% 5.177 5.87 16.04.2015 4.02% Die Rendite von über 20% ist sehr hoch, lei­der ist die Zukunft der AIG sehr unge­wiss. Eine sol­che Anleihe wür­de ich nie kau­fen — Ausfall ist jeder­zeit möglich.
86.55 3.12% Morgan Stanley Group A 6.44% 4.666 4.99 30.05.2014 0.35% Dies ist eine Anleihe die wür­de ich durch­aus noch kau­fen, eini­gen US-Banken gelang neu­lich die pri­va­te Kapitalaufnahme auch der Morgan Stanley. 
91.5 3.12% UBS AG A 5.43% 4.6 5.07 30.06.2014 -0.54% Diese nach­ran­gi­ge Anleihe war am 10.3.2009 für den Kurs von CHF 78.00 zu haben. Ich habe die­se neu­lich ver­kauft. Die UBS ist noch lan­ge nicht über dem “Berg”, daher könn­te die­se Anleihe schon bald wie­der Kursverluste einstreichen.
99.45 4.00% General Electric Capital AA 4.51% 3.85 4.23 26.08.2013 -0.45% Am 10.3.2009 brach der Kurse die­ser Anleihe auf CHF 69.25 ein. GE Capital hat eine Bilanzsumme von mehr als USD 600 Milliarden. Auch wenn die­se Anleihe seit dem 10.3.2009 steil ange­stie­gen ist, sind die Probleme bei GE Capital die­sel­ben. Der GE Finanzarm hat wahr­schein­lich vie­le fau­le Konsumkredite, wobei die Bilanz von GE Capital eine Blackbox ist. Hohe Kursrückschläge sind zu erwarten… 
97.45 2.75% HSBC Finance Corp A 4.11% 1.944 2.03 14.06.2011 0.15% Die HSBC Finance Corporation war die frü­he­re Household International, Inc,. Dies ist eine Tochter der HSBC, und kann daher nicht mit der HSBC Holding PLC ver­gli­chen wer­den. Die HSBC hät­te die­se Geld ver­schlin­gen­de Tochter fal­len las­sen kön­nen, jedoch hat dies der CEO der HSBC klar aus­ge­schlos­sen, auch wenn sich dies eini­ge HSBC Aktionäre gewünscht hät­ten. Bei der Auswahl von Anleihen kann es wich­tig sein, sol­che Holdingkonstrukte zu beach­ten! Übrigens hier lag das Kurstief bei CHF 80.50.

Die hier aus­ge­führ­te Vorgehensweise hat sei­ne bes­te Zeit schon hin­ter sich, es ist ein biss­chen wie eine Analystenempfehlung – die kom­men mit ihren Anlagevorschlägen auch immer zu spät, dies ist übri­gens wis­sen­schaft­lich nach gewissen.

Steuern

Obligationen wer­den zum Steuerkurs als Vermögen ver­steu­ert, hier­bei kann man wahr­schein­lich nicht opti­mie­ren. Der Zinscoupon kann die Steuerrechnung in die Höhe trei­ben, die­ser wird als Bruttoertrag ver­steu­ert. Wenn jemand einen ziem­lich hohen Grenzsteuersatz hat, bei­spiels­wei­se 35% oder mehr und die Aufwendungen für den Kauf und Verkauf der Obligation zusam­men bei­spiels­wei­se nicht mehr als 0.6% betra­gen, so ist es rein rech­ne­risch bes­ser, die Obligation vor dem Zinstermin zu ver­kau­fen. Beispiel:

Nennwert 50‘000.00; Zinscoupon 3% -> Jahreszins 1‘500.00
Aufwand für den Kauf/Verkauf (Transaktionskosten) -> 300.00

Für die­sen Jahreszins müss­ten 525.00 Steuer bezahlt wer­den. Wenn jedoch vor dem Zinstermin ver­kauft wird, so kos­tet es nur die Transaktionskosten von 300.00. Bei die­sem Beispiel wur­de vor­aus­ge­setzt, dass der Kurs beim Verkauf und Kauf unver­än­dert war und dass die Anleihe gera­de nach dem Zinstermin gekauft und vor dem Zinstermin ver­kauft wur­de. Allerdings kön­nen die Steuerbehörden häu­fi­ge Verkäufe kurz vor Couponverfall mög­li­cher­wei­se als Steuerumgehung taxieren.

Jeder Anleger soll­te selbst aus­rech­nen, wie sich die Couponzahlungen auf sei­ne Einkommenssteuer und bei ver­mö­gen­dem Anleger zusätz­lich auf die Vermögenssteuer aus­wir­ken. Nur wenn der Handelnde auch die Steuererklärung „im Griff hat“, kön­nen sol­che Strategien umge­setzt wer­den. Wenn jemand sein Geld in Obligationenfonds ein­be­zahlt und die Steuererklärung aus­fül­len lässt, dann wird eine sol­che Steueroptimierung kaum mög­lich sein.

Bei der Versteuerung sind Aktien klar im Vorteil, in der Schweiz müs­sen Kapitalgewinne nicht ver­steu­ert wer­den. Vielleicht ist auch für den sehr defen­si­ven Anleger rat­sam einen klei­nen Teil sei­nes Portfolios in Aktien zu inves­tie­ren als ein rei­nes Obligationenportfolio zu halten.