Vor ein paar Monaten habe ich mir das Buch “The Ivy Portfolio” gekauft. Ein Unterkapitel in diesem Buch heisst: “Winning by Not Losing”, daher der Titel dieses Eintrages. Einige Ideen aus diesem Buch könnten vielleicht für den einten oder anderen Privatanleger hilfreich sein.
The Ivy Portfolio, Mebane T. Faber und Eric W. Richardson, Wiley 2009
“How to Invest Like the Top Endowments and Avoid Bear Markets” ist der Untertitel dieses Buches.

Die ersten drei Kapitel sind ausführlich den Stiftungen der Elite-Universitäten Harvard und Yale gewidmet. Diese werden als Vorbild für das Efeu-Portfolio angeführt, letztendlich sollte der Leser mit dem erworbenen Wissen selbst ein Portfolio erstellen und managen können. Dieses sollte eine stabile Rendite unabhängig der Märkte generieren. Das Buch ist auf den amerikanischen Markt ausgerichtet, daher sind die vorgeschlagenen Portfolios für einen europäischen bzw. schweizerischen Privatanleger so nicht übertragbar. Ich werde nur einige interessante Unterkapitel kurz erwähnen.
| Teil | Titel (Deutsch) | Kapitel | Ausgewählte Unterkapitel |
|---|---|---|---|
| 1 | Konstruktion des Efeu Portfolios | The Super Endowments | Summary |
| The Yale Endowment | Of Alphas and Betas | ||
| The Harward Endowment | |||
| Building Your Own Ivy League Portfolio | Inflation Is the Enemey | ||
| Creating an All-Weather Policy Portfolio through Indexing | |||
| Implementing Your Portfolio | |||
| Rebalacing Yor Portfolio | |||
| 2 | Alternative Anlage | Private Equity | Summary |
| Hedge Funds | Summary | ||
| 3 | Aktives Management | Winning by Not Losing | The Quantitative System |
| A Rotation System | |||
| Following the Smart Money | |||
| Develop an Action Plan | Implementing Your Ivy Portfolio |
Konstruktion des Efeu Portfolios
The Super Endowments, Summary
Die grossen Stiftungen haben auf Grund ihres aktiven Asset Management, eine Mehrrendite gegenüber den kleinen Stiftungen, die vermehrt eine passive buy-and-hold Strategie fahren.
Bei den grossen Stiftungen ist die Gewichtung von traditionellen Anlagen geringer, umsomehr sind die Anteile an realen (Immobilien, Grundstücke usw.) und alternativen Anlagen höher.
Of Alphas und Betas
Bei aktiv gemanagten Geldanlagen werden des Öfteren die zwei griechischen Buchstaben Alpha und Beta benutzt. Ein ETF, der einen Index nachbildet, kann diesen nicht “schlagen”, daher generiert der passive ETF nur Beta. Ein Aktienfonds hat einen Benchmark, wenn der Fondsmanager eine Mehrrendite über diesem Benchmark erzielt, so hat er ein positives Alpha generiert. Ein aktiv gemanagter Aktienfonds hat in der Regel viel höhere Gebühren als ein passiver ETF, dafür erwartet der Anleger von diesem Fonds ein entsprechendes positives Alpha.
Building Your Own Ivy League Portfolio
Inflation Is the Enemey (Inflation ist Ihr Feind)
Dass die Renditen der Asset Klassen sehr unterschiedlichen während der Zeitperioden von hoher bzw. tiefer Inflation ausfallen ist wohl bekannt. Folgende Renditen wurden während der Inflationsperioden von 1972–2007 erzielt:
| U.S. Aktien | Nicht U.S. Aktien | U.S. Anleihen | Rohstoffe | Immobilien (US-Reits) | Inflation | |
|---|---|---|---|---|---|---|
| Hohe Inflation (1972–1981) | 8.46% | 12.54% | 3.27% | 19.16% | 11.16% | 8.70% |
| Tiefe Inflation (1982–2007) | 14.11% | 14.24% | 10.84% | 12.65% | 12.83% | 3.15% |
Meine Bemerkung: Mit nur zwei Teilzeiträumen ist eine solche Aussage wie in der obigen Tabelle ein bisschen fahrlässig.
Daraus ist ersichtlich, dass Rohstoffe ein guter Schutz vor Inflation sind und das Anleihen erwartungsgemäss in Zeiten von hoher Inflation kaum noch Erträge abwerfen.
Creating an All-Weather Policy Portfolio through Indexing
Die folgende Zahlen bestätigen, dass Stock-Picking nur in seltenen Fällen zu einem Alpha führen. Eric Crittenden und Cole Wilcox haben den Russel 3000 seit 1983 auf die Aktienrenditen untersucht. Der Russel 3000 beinhaltet die 3000 grössten U.S. Firmen. Über diese Zeitperiode hatten 40% der Aktien eine negative Rendite, 20% verloren fast ihren gesamten Wert und 10% Aktien legten über 500% zu. Zusammengefasst konnten nur 36% der Aktien ihren Index schlagen, d.h. 64% der Aktien performten schlechter als der Russel 3000.
Implementing Your Portfolio (Umsetzung des Portfolios)
Es werden unterschiedliche Portfolios mit mehr oder weniger Asset Klassen erläutert. Die folgende Tabelle enthält das einfachste Portfolio.
| Ivy Portfolio | ETF | Expense Ration | Anbieter | Bermerkung | |
|---|---|---|---|---|---|
| U.S. Aktien | 20% | VTI | 0.07% | Vanguard | MSCI US Breiter Markt Index, über 3600 Titel |
| Nicht U.S. Aktien | 20% | VEU | 0.25% | Vanguard | FTSE All-World ex-US ETF, zirka 2200 Titel |
| Anleihen | 20% | BND | 0.11% | Vanguard | Total Anleihen Mark, Firmen- und Staatsanleihen, Government Mortage-Backed usw. Die Anleihen-Index deckt fast alles ab. |
| Immobilien | 20% | VNQ | 0.12% | Vanguard | MSCI US REIT |
| Rohstoffe | 20% | DBC | 0.83% | PowerShares | Deutsche Bank Liquid Commodity Index (DBLCI). Preisentwicklung von sechs Rohstoffen ab: Rohöl (WTI), Heizöl, Aluminium, Gold, Weizen und Mais. |
Die Aufteilung entspricht 40% Aktien und je 20% in die anderen Asset Klassen. Dieses Portfolio ist natürlich für unseren EUR- und CHF-Markt nicht geeignet. Die alternativen Anlagen sind in diesen Portfolios nicht vertreten.
Rebalacing Yor Portfolio
Das Portfolio sollte jährlich überprüft werden und eventuelle ein Rebalancing durchgeführt werden. Viel steht in diesem Unterkapitel noch über Optimierung von Steuern, was aber nicht auf die Schweiz übertragbar ist.
Alternative Anlagen
Private Equity
Für einen Privatanleger ist der Zugang zu Private Equity eher schwierig. Normalerweise kann nur mit einem hohen minimalen Betrag in diese Asset Klasse investiert werden. Es gibt Private Equity ETFs, diese investieren aber meistens in die Aktien von Firmen, die in Private Equity Firmen involviert sind, es ist damit eine indirekte Investition.
Hedge Funds
Auch die Investitionen in Hedge Funds erweisen sich für die nicht sehr reichen Privatanleger als schwierig. Es gibt auch ETFs, welche diese Asset Klasse abdecken, beispielsweise den db HEDGE FUND INDEX ETF (ISIN: LU0328476337).
Aktives Management
Winning by Not Losing
Schon fast regelmässig gibt es Blasen, die nach dem Platzen, die Aktien 40% bis 80% abstürzen lassen. Wenn jemand einen Verlust von 75% einfährt, braucht er danach einen Gewinn von 300% um diesen Verlust auszugleichen. Seit 1900 verlor der Dow Jones mehr als 30 Mal über 20% und 10 Mal verlor er über 40%. Wie wäre es schön diese Verluste vermeiden zu können, wobei Sie dabei Ihr grösster Feind sind.
The Quantitative System
Mit einem mechanischen System können die persönlichen Emotionen bei der Kauf- bzw. Verkauf-Entscheidung eliminiert werden. Das vorgeschlagene System basiert auf dem gleitenden Durchschnitt (SMA). Oftmals erzeugen solche Systeme viele Kauf bzw. Verkaufs-Signale, was hohe Transaktionskosten verursacht. Das Buch schlägt ein System vor, mit einem gleitenden Durchschnitt basierend auf Monatsdaten.
| S&P 500 | Mechanisches Timing | |
|---|---|---|
| Rendite per annum | 9.21% | 10.45% |
| Volatilität | 17.87% | 12.02% |
| Sharpe 4% | 0.29 | 0.54 |
| Maximaler Verlust | -83.66% | -50.31% |
| Bestes Jahresrendite | 52.88% | 52.40% |
| Schlechteste Jahresrendite | -43.86% | -26.87% |
Aus der Tabelle wird ersichtlich das die Rendite beim mechanischen System gegenüber buy-and-hold zirka 1% höher ausfällt. Zudem ist die Volatilität, d.h. das Risiko um zirka 5% geringer. Wie das System funktioniert:
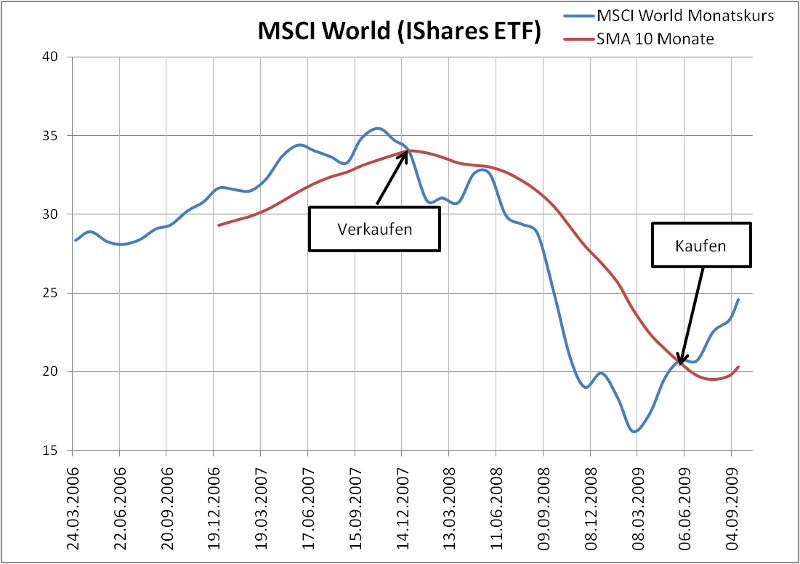
- Kaufregel: Wenn Kurs > 10-Monat SMA
- Verkaufregel: Wenn Kurs 10-Monat SMA
Aus dem oben dargestellten Diagramm ist ersichtlich, warum die Volatilität mit diesem mechanischen System geringer ausfällt. Bei hohen Kursrückschlägen ist der Anleger in der Regel nicht mehr long positioniert. Anderseits kann von einem raschen Anstieg der Kurse, wie diese seit dem 9.03.2009 stattfindet, erst mit einer Verzögerung profitiert werden. Letztendlich “glättet” ein solches System die hohen Verluste bzw. Gewinne. Der 10-Monat-SMA ist nicht die einzige richtige Lösung, beispielsweise könnte ein 8‑Monat-SMA durchaus für einen anderen Index bzw. andere Zeitperiode besser geeignet sein.
Mit dem Analysis-Tool von Swissquote können Sie problemlos ein solches MAV (SMA) Chart darstellen lassen.
A Rotation System (Das Rotationssystem)
Im oben dargestellten System kann es vorkommen, dass man zu einer bestimmten Zeit nur mit 20% in eine Asset Klasse investiert ist und 80% Cash hält. Es gibt Anleger, die einem Rotationssystem folgen, dabei werden die durchschnittlichen Renditen in Perioden von 1, 3, 6 oder 12 Monate/n berechnet. Die Wahl der Periode ist dabei nicht so entscheidend, im Buch werden gar alle Perioden für die Renditenberechnung der Asset Klassen vorgeschlagen. Danach erfolgt die Investitionen für die nächste Periode in die X Asset Klassen mit den höchsten Renditen. Beim einfachen Portfolio würden beispielsweise je 50% in die zwei Asset Klassen investiert, die in den letzten Perioden die höchsten Renditen abwarfen. Es wird nicht empfohlen 100% auf eine Asset Klasse zu setzen, andernfalls ergeben sich geringerer Diversifikationseffekt und höhere Risiken. Beim Fünf-Asset-Klassen Portfolio wird eine minimale Aufteilung in 2 oder 3 Asset Klassen empfohlen.
Following the Smart Money (Dem intelligenten Geld folgen)
Das Buch schlägt hier eine Stock-Picking Strategie vor, indem man den besten Fondsmanagern mit Verzögerung über die Schultern schaut.
In den USA müssen die Anlagefonds ab einem Anlagevermögen vom mehr USD 100 Millionen ihre Assets quartalsweise der U.S. Securities and Exchange Commission (SEC) melden. Diese Assets können innerhalb 45 Tage nach Quartalsschluss in der EDGAR Datenbank eingesehen werden. Es werden aber nur Long-Positionen ausgewiesen, d.h. keine Short-Positionen und auch keine Derivate.
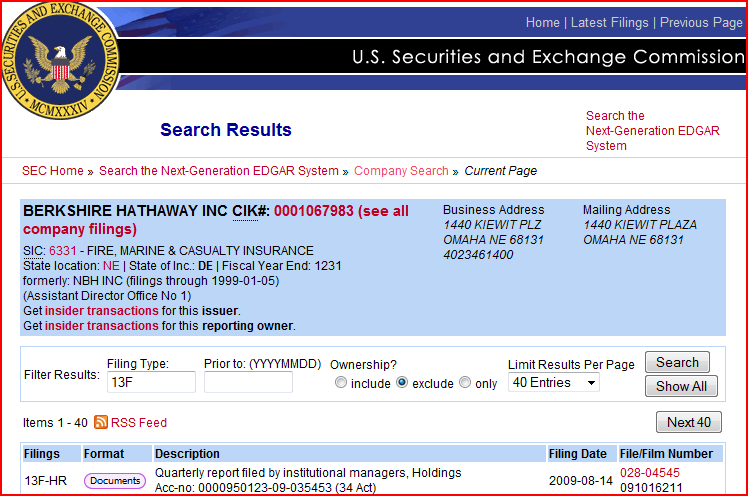
In EDGAR kann beispielsweise die gehaltenen Positionen von Berkshire Hathaway (CIK-Nr.: 0001067983) ermittelt werden.
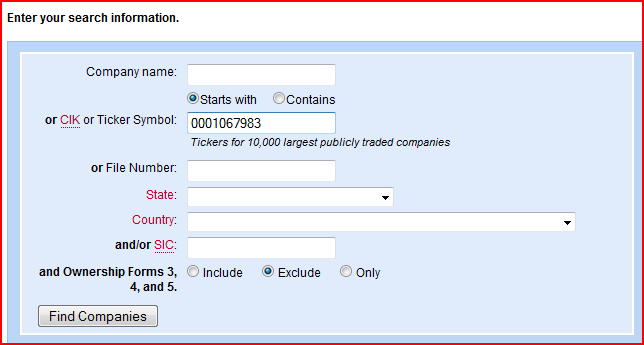
Im Feld “Filling Type” wird nur “13F” eingegeben und nach der Suche steht der neuste Quartals-Report zuoberst auf der Liste. Damit können die gehaltenen Aktienpositionen von Warren Buffett’s Berkshire erfahren werden.
Das Buch enthält eine Liste von Fonds, die sich für eine solche Prozedur eignen. Es gibt auch eine kostenpflichtige Website AlphaClone, welche diese Alpha-Selektion durchführt.
Develop an Action Plan, Implementing Your Ivy Portfolio
Dieses Unterkapitel gibt eine schrittweise Anweisung für die Implementierung Ihres Portfolios. Beispielsweise müssen Sie gemäss Ihrem Risiko/Rendite Profil herausfinden, wie hoch Sie die einzelnen Asset Klassen in Ihrem Portfolio gewichten wollen. Dieses Kapitel enthält nur zirka 7 Seiten, daher ist es mehr eine Zusammenfassung der vorhergehenden Kapitel.
Meine Buchkritik
Investieren wie die beiden Stiftungen Harvard und Yale, ist für den Privatanleger nicht möglich, daher wird dieses Buch dem Untertitel “How to Invest Like the Top Endowments and Avoid Bear Markets” nur zum Teil gerecht. Zudem haben auch die beiden Stiftungen im letzten Geschäftsjahr erhebliche Verluste eingefahren. Mit einem Verlust von 24.6% ging am 30.6.2009 das Geschäftsjahr der Yale-Stiftung zu Ende, gar einen Verlust von 27.3% erlitt im gleichen Zeitraum die Harvard-Stiftung. Zudem haben beide Stiftungen sehr viel Geld in eher illiquiden Anlagen was viele Privatanleger sicherlich vermeiden wollen.
Die Ratschläge für die Vermeidung eines Bärenmarktes können eher von einem Privatanleger umgesetzt werden. Zurzeit sind Investitionen in Alternative Anlagen wie Hedge Fonds oder Private Equity für den nicht reichen Privatanleger eher schwierig, trotzdem widmet das Buch zirka 25% des Inhaltes diesem Thema. Gleichwohl kann ich dieses Buch empfehlen, da er dem Leser reale ETF-Portfolio vorschlägt, natürlich müssten diese auf den schweizerischen Markt angepasst werden. Zu diesem Buch gibt es noch die interessante Website “The Ivy Protfolio”.